Important aspects of thermal insulation solutions for comfort in summer
| 24 May 2007 - Comments (0) | Construction |
We explained before the parameters, such as λ and U-value, that are important when comparing thermal insulation solutions. Those parameters are concerned about how much heat can pass through the material.
To evaluate the behavior of a material in summer, we also need to know how fast heat can pass through the material. And, as it is related, we need to know how much heat can be stored in the material. In this article, we look at the parameters that are important to understand those two aspects.
Role of thermal insulation
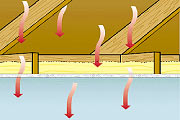
Thermal insulation prevents heat to flow between indoor and outdoor climate. The goal is to maintain a more or less constant indoor temperature while outdoor temperature varies greatly, during the day and over the year.
In winter, spring and fall, it is not only interesting to keep indoor heat, but it is also important to capture outdoor heat that can exist during the day to reuse it freely during the night when temperature drops. This can suppress the need to use the heating system at night and therefore shorten the heating period.
During summer, on the contrary, we want to prevent outdoor heat to come indoor and we want the indoor heat to dissipate during the night to cool down the house before the next hot day.
It is to understand those two aspects, storage of heat and heat protection that we need to explain some fundamental properties of materials. It might look a bit dry but it is really enlightening.
Parameters affecting the capacity to store heat
Density (ρ)
Density of a material represents its mass per unit of volume. Lightweight insulation materials such as polystyrenes or mineral wools are not dense while concrete or clay is much more dense.
ρ = m / V (in kg/m3)
Intuitively, we can already guess that there is a relation between density and heat storage. But density is not enough to quantify that.
Specific heat capacity (c)
Specific heat capacity of a material measures the heat energy required to raise the temperature of the material by one degree per unit of weight (in J/kg.K). We can see it as a measure of how much heat a material can absorb per unit of weigth.
Volumetric heat capacity or thermal inertia (C)
Specific heat capacity is per unit of weight. A more interesting measure of heat capacity is per unit of volume. It is called the volumetric heat capacity or simply, for construction materials, thermal inertia. It is equals to the specific heat capacity (c) times the density (ρ).
C = c.ρ (in J/m3K)
Thermal inertia represents how much heat can be stored in a given volume of a building section.
Parameters affecting the speed of heat transfer
Thermal diffusivity (a)
Having defined the concept of thermal inertia (C) and thermal conductivity (λ, in a previous entry) we can now define one very important concept for the performance of thermal insulation in summer: thermal diffusivity indicates how easy a material will undergo temperature change. Thermal diffusivity is equal to thermal conductivity (λ) divided by thermal inertia (C).
a = λ / C (in m²/s)
While thermal conductivity (λ) determines how much heat will flow in a material, thermal diffusivity (a) determines how rapidly heat will flow within it. Looking at the equation above, one can see that for materials with similar λ, heat will flow faster in those with less thermal inertia (smaller C).
Thermal time constant or thermal phase lag
Based on thermal diffusivity, another interesting parameter is time constant. It is the time it takes for a change in surface temperature to reach a certain depth of a building component. Knowing the thickness of a material (d), time constant can be used to know, how long it will take for the heat wave, to go through the material. It is also called thermal phase lag. It is equal to the thickness squared divided by the thermal diffusivity.
t = d² / a (time in second)
Time constant or phase lag determines how long it takes for heat to go through a given thickness of a material.
Thermal effusivity (b)
Here the last parameter we will introduce for completion. Thermal effusivity represents the capacity of a material to absorb and release heat and characterises how easily heat can be absorbed at the surface of a material.
b = (λ.C)1/2 (in W/m².K.s1/2)
Thermal effusivity determines how easily heat can be exchanged at the surface of a material. Materials with high thermal effusivity (such as metals) are not good to store heat because heat will very quickly dissipate outside as soon as temperature drops. They cannot hold heat for long. On the contrary, material with high thermal inertia but low thermal effusivity, such as clay or stone will hold heat much longer.
Conclusion
Two parameters are really interesting to evaluate the behavior of a thermal insulation solution outside of winter: thermal inertia and thermal phase lag.
Thermal inertia quantifies the capacity of a material to store surrounding heat and to release it when surrounding temperature drops. Thermal inertia as heat storage concerns mainly heavy building components such as concrete, clay blocks or bricks and can be a key component for comfort in summer. We will detail that aspect in a follow up article.
Thermal phase lag is the time is takes for heat to go through the thickness of a building component. It depends on the thickness, the thermal conductivity and the thermal inertia of the material. The time will be greater for material with low thermal conductivity and high thermal inertia. Thermal phase lag is the key aspect for insulation materials in summer.
In an upcoming article, we will see the implication of thermal phase lag on the choice of thermal insulation material for comfort in summer.
